Differential Evolution (DE)

for Continuous Function Optimization (an algorithm by Kenneth Price and Rainer Storn)

History

Differential Evolution grew out of Ken Price's attempts to solve the Chebychev Polynomial fitting Problem that had been posed to him by Rainer Storn. A breakthrough happened, when Ken came up with the idea of using vector differences for perturbing the vector population. Since this seminal idea a lively discussion between Ken and Rainer and endless ruminations and computer simulations on both parts yielded many substantial improvements which make DE the versatile and robust tool it is today. The "DE community" has been growing since the early DE years of 1994 - 1996 and ever more researchers are working on and with DE. Those scientists who contributed actively to this homepage are listed at the bottom in alphabetical order. It is the strong wish of Ken and Rainer that DE will be developed further by scientists around the world and that DE may improve to help more users in their daily work. This wish is the reason why DE has not been patented in any way.

Basics

DE is a very simple population based, stochastic function minimizer which is very powerful at the same time. DE managed to finish 3rd at the First International Contest on Evolutionary Computation (1stICEO) which was held in Nagoya, may 1996. DE turned out to be the best genetic type of algorithm for solving the real-valued test function suite of the 1st ICEO (the first two places were given to non-GA type algorithms which are not universally applicable but solved the test-problems faster than DE). The crucial idea behind DE is a scheme for generating trial parameter vectors.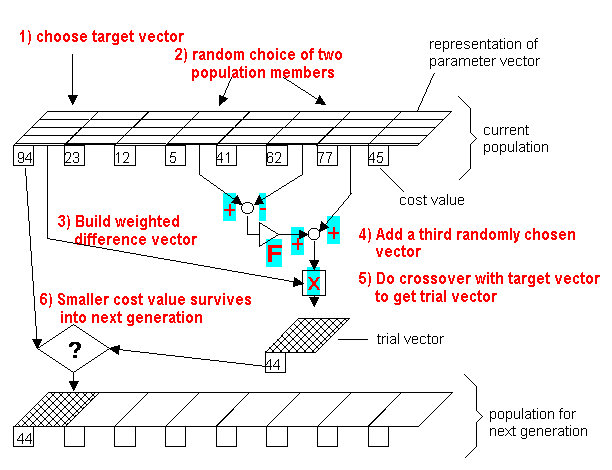 Basically, DE adds the weighted difference between two population vectors to a third vector. This way no separate probability distribution has to be used which makes the scheme completely self-organizing. For further details see the literature page.

Practical Advice

If you are going to optimize your own objective function with DE, try the following settings for the input file first: Choose method e.g. DE/rand/1/exp, set the number of parents NP to 10 times the number of parameters, select weighting factor F=0.8 and crossover constant CR=0.9. Make sure that you initialize your parameter vectors by exploiting their full numerical range, i.e. if a parameter is allowed to exhibit values in the range [-100, 100] it's a good idea to pick the initial values from this range instead of unnecessarily restricting diversity. If you experience misconvergence you usually have to increase the value for NP, but often you only have to adjust F to be a little lower or higher than 0.8. If you increase NP and simultaneously lower F a little, convergence is more likely to occur but generally takes longer, i.e. DE is getting more robust (there is always a convergence speed/robustness tradeoff).

DE is much more sensitive to the choice of F than it is to the choice of CR. CR is more like a fine tuning element. High values of CR like CR=1 give faster convergence if convergence occurs. Sometimes, however, you have to go down as much as CR=0 to make DE robust enough for a particular problem. If you choose binomial crossover like, DE/rand/1/bin, CR is usually higher than in the exponential crossover variant (in this example DE/rand/1/exp). Still, F and CR are both generally in the range [0.5, 1.] for most problems we've encountered. Keep in mind that different problems usually require different settings for NP, F and CR (have a look into the different papers to get a feeling for the settings). If you still get misconvergence you might want to try a different method. We mostly use DE/rand/1/... or DE/best/2/... (for the latter F=0.5 is the standard choice). The crossover method is not so important although Ken Price claims that binomial is never worse than exponential. In case of misconvergence also check your choice of objective function. There might be a better one to describe your problem. Any knowledge that you have about the problem should be worked into the objective function. A good objective function can make all the difference.

DE-Applet

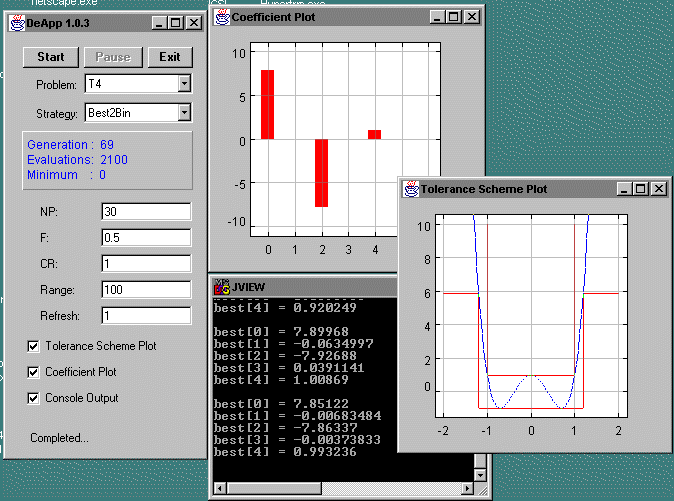
DE is demonstrated here by example of the polynomial fitting problem (see techreport by Rainer and Ken). The task is to fit a polynomial of a certain degree into the tolerance scheme indicated by the red lines. At x-values +/- 1.2 the polynomial must be higher than Tk(x) with Tk(x) being the Chebychev Polynomial of degree k. The constraint at +/- 1.2 can't be seen in the animation as it is fairly large (~5.9 for T4(x) and ~72.661 for T8(x)). The cost function to be minimized is the sum of squared errors. Depending on the DE-variant the T4 problems takes several thousand function evaluations to be solved. T8 needs about five to ten times as much. The applet was programmed by Mikal Keenan (DE) and Rainer Storn (GUI). Fetch the source code DEApplet1.java and DEApplet1.html to see what we have done.

Java Code

In order to make it easy to do DE optimization on every platform with the support of graphics a Java application of a DE optimizer has been written. The current version (1.0.3) runs now both in JDK 1.0.2 as well as JDK 1.1.7. The code has been enriched with the magnificent plotting capabilities of ptplot, written by Edward A. Lee and Christopher Hylands from the University of California, Berkeley. Now it is possible to zoom in and out of the plots as the optimization is ongoing. A corrected version of the code documentation is also available.

C Code

To play with DE one only needs the main routine de36.c (version 3.6), the corresponding header file de.h along with some example like the polynomial fitting problem (filename e.g. dj9.c)and the corresponding input file (filename e.g. dj9.dat).

Compile the example by using e.g.

CC de.c dj9.c -o dj9

and run the example by typing

dj9 dj9.dat dj9.out.

Most recently Peter Turney updated the C-code above to make it more compatible to Visual C++ 6.0 and also to Unix-based C-compilers.

Matlab Code

Thanks to Arnold Neumaier and Rainer Storn the DE strategy is also available in MATLAB code. The vectorized programming, necessary to make MATLAB code reasonably fast, didn't allow for exponential crossover, so binomial crossover is used here. The DE strategy is illustrated in a demo package. 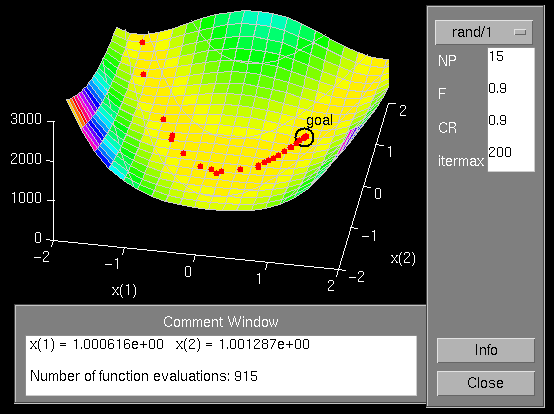The demo package is intended to let the user experiment with the different DE-strategies and control variable settings to obtain experience how DE reacts to the different settings. Currently a trace of the best population member of each DE-iteration is displayed as shown in the picture above. A flag-variable in the plot-supporting function xplt.m allows, however, to show the trace of all population members simultaneously. The m-files necessary to run the DE-demo in MATLAB are the demo shell dedemov.m, the actual DE-minimizer devec.m and the plot-supporting function xplt.m. If you want to use the DE-strategy in MATLAB for your own purposes it is better to use devec3.m which minimizes an externally defined objective function, e.g. rosen.m. Use the help function in MATLAB to obtain the details on how to use devec3.m. Two helper files, run1.m and run2.m show you how to work with devec3.m more conveniently.

Scilab Code

There is also a Scilab version of DE written by Walter Di Carlo. Scilab is a public domain clone of MATLAB

PSather Code

DE is perfectly suited for parallel computation which already has found an implementation in PSather, a parallel object oriented language being developed at ICSI. The code was developed by Claudio Fleiner.

C++ Code

You can also get a completely object oriented C++ version of DE by fetching De37.zip. The code has been developed by Mikal Keenan with VisualC++ 7.0. Another C++ version, written by Lester Godwin in Visual C++ 5.0, is available as devcpp.zip.

Fortran90 Code

Another contribution is a Fortran90 version of DE developed by Prof. Feng-Sheng Wang and his students.

Python Code

A recent addition is a Python version of DE developed by James R. Phillips.

Labview Code

The latest contribution is a Labview version of DE developed by Franz Josef Ahlers.

Demo-Programs

If you happen to have access to a DOS-PC and have the graphics driver egavga.bgi from Borland's C++ library (version 3.1) you have all the requirements to get two little demo programs running which show DE at work. These programs are dedemo.exe and dedemo2.exe (fetch them via SHIFT+"Click" in Netscape) along with their data files demo.dat and demo2.dat. After placing these files in the pertinent directory, all you have to do is type

dedemo demo.dat

which shows you the polynomial fitting problem, or

dedemo2 demo2.dat

which visualizes DE working on Rosenbrock's saddle.

You can even manipulate the .dat files to experiment with different parameter values. Note however, that the demo programs are not crash proof, i.e. if you exceed certain limits for the parameters the programs will crash. So it's best to change e.g. only the number of parents NP < 200, weighting constant F ex [0,1] and crossing over factor CR ex [0,1] but NOT to change the number of parameters D. All the other parameters might be safely changed if the parameters are > 0. But remember: "everything that is free comes with no guarantee".