FIR-design with maximally flat passband response
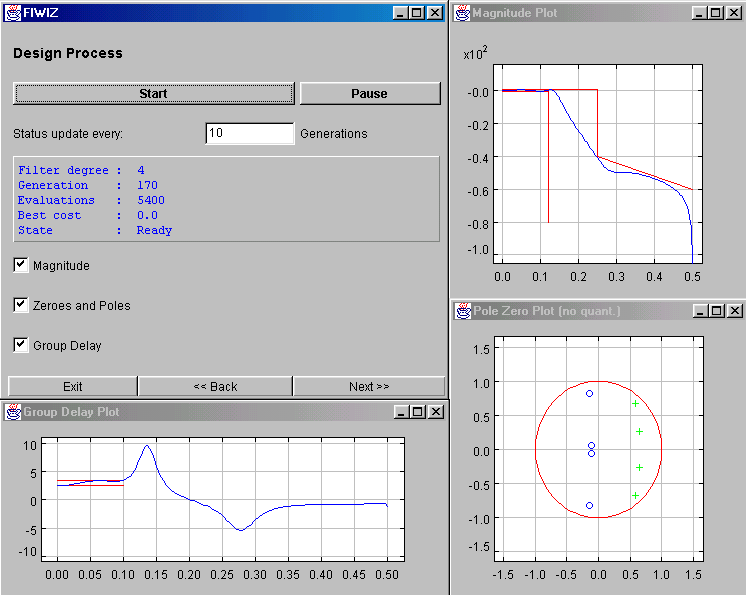
Features for Z-Plane design
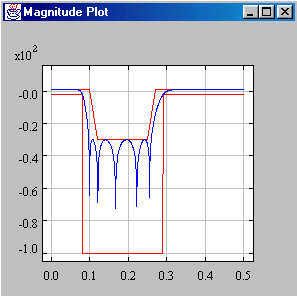
Arbitrary magnitude constraints
This feature allows for multiband filters, differentiators,
sinc compensated filters and others. See a multiband filter and a differentiator as
examples below. The y-axis is the magnitude in dB and the x-axis denotes the normalized
frequency:
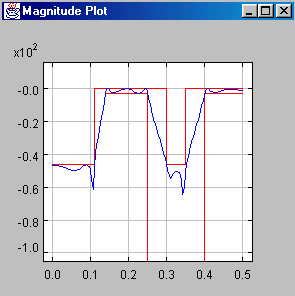
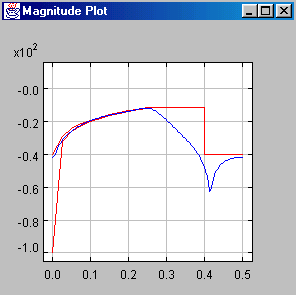
If the upper and lower constraint are equal then a least squares fit will be computed.
For a simple example see the next picture:
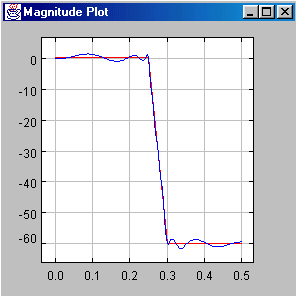
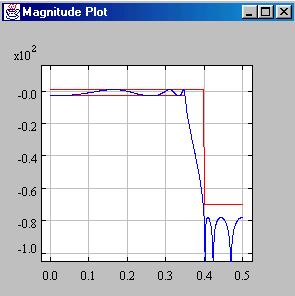
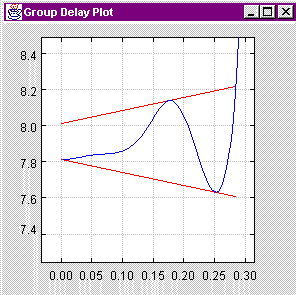
Arbitrary group delay constraints
Applications are mainly classical lowpass, highpass, bandpass, and bandstop filters
which should exhibit approximately linear phase in the passband(s) but not necessarily
in the stopband(s). This way the filter degree can often be reduced considerably compared
to exactly linear phase FIR filters. See an IIR graphics codec as an example:
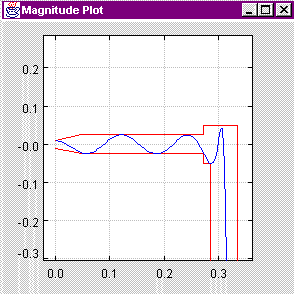
Coefficient Quantization
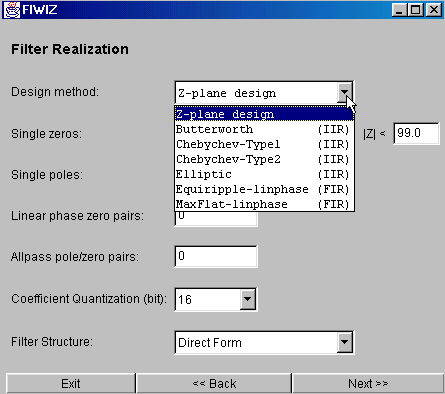
FIWIZ allows to include coefficient quantization in the filter design, i.e.
quantization is incorporated into the design as opposed to quantizing the coefficients
after the filter has been designed with high precision coefficients. This feature is
only available for the Z-plane design. For the classical filter design methods
(butterworth, chebyshev, inverse chebyshev, elliptical) the quantization is applied
after the filter has been designed.
See an example screen shot of the corresponding input screen:
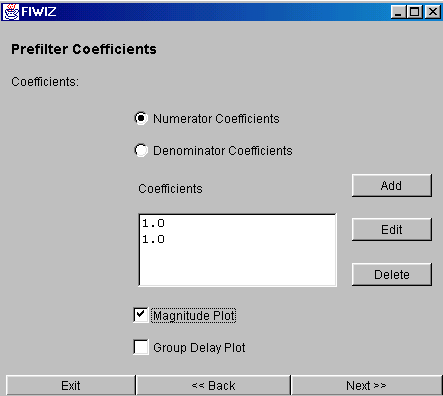
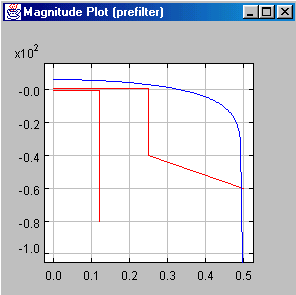
Definition of a prefilter with constant coefficients
Defining a prefilter has many applications like presetting specific zeroes to suppress DC or the
50/60Hz powerline frequency, accomodating filters which are already in a design and cannot be removed,
or setting a frequency response to equalize. A well-known example for the latter is sinc compensation
needed for D/A-conversion. An example for the input screen is shown below:
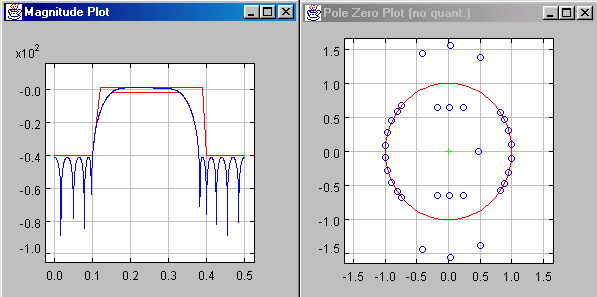
Minimum phase filters
Some applications don’t require any specific phase response, and hence the filter
degree can be minimized by using minimum phase filters. Minimum phase can be easily
enforced by constraining the zero radii to be inside or on the unit circle.
Minimum delay and fractional delay filters
By allowing to freeze the group delay constraints FIWIZ assists in the design of
minimum delay or fractional delay filters.
Other features
Allpass design
The phase of an existing IIR-filter can be linearized with an allpass approach.
IIR-filters with reduced impulse response length
By constraining the pole radii the impulse response length of an IIR filter can be reduced.
Output of poles and zeroes
The results file of FIWIZ contains not only the filter coefficients of the direct form 1
(or 2) or first and second order sections, but also the pole and zero radii as well as angles.
MATLAB friendly output format
FIWIZ's output can be directly posted on to MATLAB's command line interface for further
analysis.
Storage and retrieval of configuration files
The settings of constraints and design parameters can be stored and retrieved so that
there remains only little retyping if a previous filter design shall be altered.
Platform independence through JAVA technology
FIWIZ is an application that has been written completely in
JAVA, and hence it runs on any platform which
supports the JAVA virtual machine (e.g. Windows 95/89/NT, Solaris, or Mac OS).
First you have to get the Java runtime environment (JRE) for your platform.
It allows so-called Java Bytecode to run on your machine (this is the format which
Fiwiz comes in).
Download the JRE1.1x for
Windows 95/89/NT, Solaris or for
Mac OS at no charge. Windows users may also use the locally available
JRE1.18. Solaris users may download
the locally available Solaris-JRE1.1.7.
If you are new to Java you might want to
have a look at this tutorial. For convenience FIWIZ is also available as a Windows® .exe version.
Wizard based approach
FIWIZ's wizard based approach makes using FIWIZ almost self-explanatory. The sequence of
operations is evident.
Versatile plotting
Thanks to the richly featured plotting engine
PtPlot by the University
of Berkeley you can watch various data online while the filter is designed. Resizing of the
plots as well as zooming in and out is possible.
If you want to know more about Fiwiz you can download the user manual in
A4 format. If you want to try the code first you can
download a demo version (for tha Java virtual machine)
of Fiwiz version 2.4 or the Windows® .exe version (also version 2.4).
Note that this demo version
will neither print out the zeroes and poles nor the coefficients.
Also the pole/zero plot offers no zooming capability.
Unlike in previous demo
versions the number of zeroes, poles, and linear phase zero pairs is not restricted anymore with
respect to the full version.
For more information or suggestions for improvement send me
an E-mail.
Fiwiz is commercially available (for price information see the appropriate digibuy buttons).
You can purchase via credit card by using a
secure link. After payment you can immediately download the code which is
zip-compressed for faster delivery.
(JVM executable) 
(Windows® .exe Version) 




 Version 2.4
Version 2.4